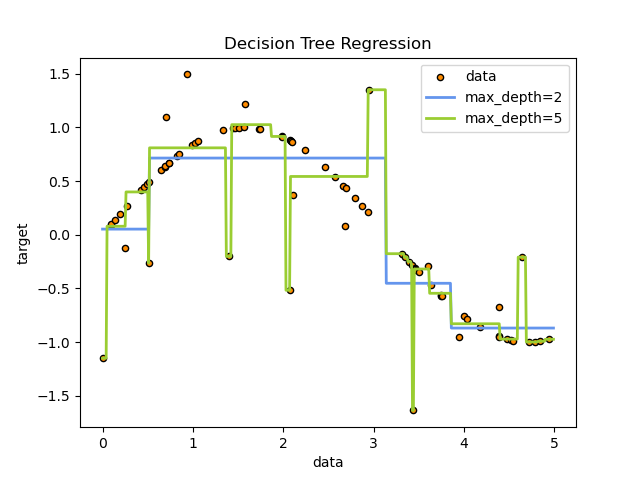
Decision Trees (DTs) are a non-parametric supervised learning method used for classification and regression . The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features. A tree can be seen as a piecewise constant approximation.
For instance, in the example below, decision trees learn from data to approximate a sine curve with a set of if-then-else decision rules. The deeper the tree, the more complex the decision rules and the fitter the model.

Some advantages of decision trees are:
The disadvantages of decision trees include:
DecisionTreeClassifier is a class capable of performing multi-class classification on a dataset.
As with other classifiers, DecisionTreeClassifier takes as input two arrays: an array X, sparse or dense, of shape (n_samples, n_features) holding the training samples, and an array Y of integer values, shape (n_samples,) , holding the class labels for the training samples:
>>> from sklearn import tree >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, Y)
After being fitted, the model can then be used to predict the class of samples:
>>> clf.predict([[2., 2.]]) array([1])
In case that there are multiple classes with the same and highest probability, the classifier will predict the class with the lowest index amongst those classes.
As an alternative to outputting a specific class, the probability of each class can be predicted, which is the fraction of training samples of the class in a leaf:
>>> clf.predict_proba([[2., 2.]]) array([[0., 1.]])
DecisionTreeClassifier is capable of both binary (where the labels are [-1, 1]) classification and multiclass (where the labels are [0, …, K-1]) classification.
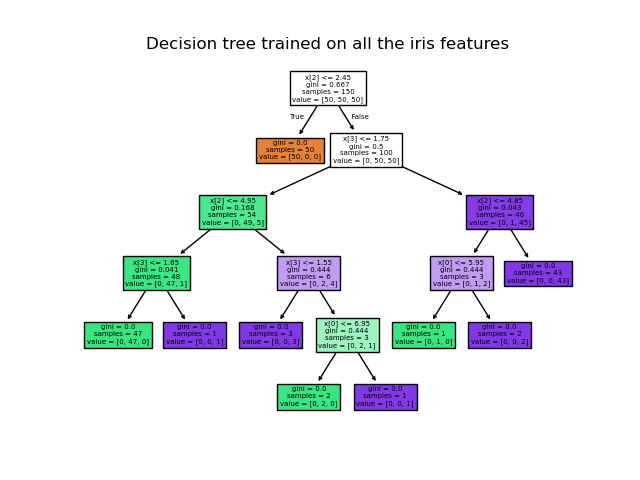
Using the Iris dataset, we can construct a tree as follows:
>>> from sklearn.datasets import load_iris >>> from sklearn import tree >>> iris = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y)
Once trained, you can plot the tree with the plot_tree function:
>>> tree.plot_tree(clf) [. ]
Alternative ways to export trees#
We can also export the tree in Graphviz format using the export_graphviz exporter. If you use the conda package manager, the graphviz binaries and the python package can be installed with conda install python-graphviz .
Alternatively binaries for graphviz can be downloaded from the graphviz project homepage, and the Python wrapper installed from pypi with pip install graphviz .
Below is an example graphviz export of the above tree trained on the entire iris dataset; the results are saved in an output file iris.pdf :
>>> import graphviz >>> dot_data = tree.export_graphviz(clf, out_file=None) >>> graph = graphviz.Source(dot_data) >>> graph.render("iris")
The export_graphviz exporter also supports a variety of aesthetic options, including coloring nodes by their class (or value for regression) and using explicit variable and class names if desired. Jupyter notebooks also render these plots inline automatically:
>>> dot_data = tree.export_graphviz(clf, out_file=None, . feature_names=iris.feature_names, . class_names=iris.target_names, . filled=True, rounded=True, . special_characters=True) >>> graph = graphviz.Source(dot_data) >>> graph
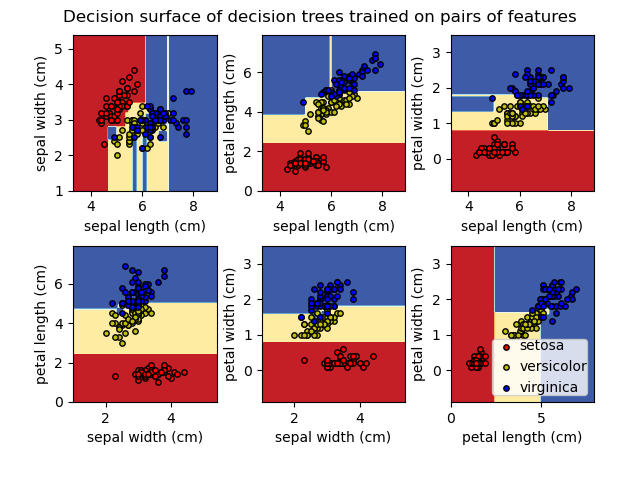
Alternatively, the tree can also be exported in textual format with the function export_text . This method doesn’t require the installation of external libraries and is more compact:
>>> from sklearn.datasets import load_iris >>> from sklearn.tree import DecisionTreeClassifier >>> from sklearn.tree import export_text >>> iris = load_iris() >>> decision_tree = DecisionTreeClassifier(random_state=0, max_depth=2) >>> decision_tree = decision_tree.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=iris['feature_names']) >>> print(r) |--- petal width (cm) | |--- class: 0 |--- petal width (cm) > 0.80 | |--- petal width (cm) | | |--- class: 1 | |--- petal width (cm) > 1.75 | | |--- class: 2

Decision trees can also be applied to regression problems, using the DecisionTreeRegressor class.
As in the classification setting, the fit method will take as argument arrays X and y, only that in this case y is expected to have floating point values instead of integer values:
>>> from sklearn import tree >>> X = [[0, 0], [2, 2]] >>> y = [0.5, 2.5] >>> clf = tree.DecisionTreeRegressor() >>> clf = clf.fit(X, y) >>> clf.predict([[1, 1]]) array([0.5])
A multi-output problem is a supervised learning problem with several outputs to predict, that is when Y is a 2d array of shape (n_samples, n_outputs) .
When there is no correlation between the outputs, a very simple way to solve this kind of problem is to build n independent models, i.e. one for each output, and then to use those models to independently predict each one of the n outputs. However, because it is likely that the output values related to the same input are themselves correlated, an often better way is to build a single model capable of predicting simultaneously all n outputs. First, it requires lower training time since only a single estimator is built. Second, the generalization accuracy of the resulting estimator may often be increased.
With regard to decision trees, this strategy can readily be used to support multi-output problems. This requires the following changes:
This module offers support for multi-output problems by implementing this strategy in both DecisionTreeClassifier and DecisionTreeRegressor . If a decision tree is fit on an output array Y of shape (n_samples, n_outputs) then the resulting estimator will:
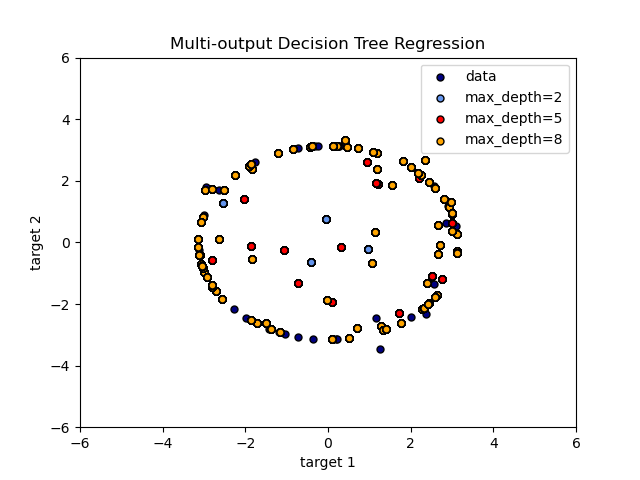
The use of multi-output trees for regression is demonstrated in Multi-output Decision Tree Regression . In this example, the input X is a single real value and the outputs Y are the sine and cosine of X.
The use of multi-output trees for classification is demonstrated in Face completion with a multi-output estimators . In this example, the inputs X are the pixels of the upper half of faces and the outputs Y are the pixels of the lower half of those faces.

In general, the run time cost to construct a balanced binary tree is \(O(n_n_\log(n_))\) and query time \(O(\log(n_))\) . Although the tree construction algorithm attempts to generate balanced trees, they will not always be balanced. Assuming that the subtrees remain approximately balanced, the cost at each node consists of searching through \(O(n_)\) to find the feature that offers the largest reduction in the impurity criterion, e.g. log loss (which is equivalent to an information gain). This has a cost of \(O(n_n_\log(n_))\) at each node, leading to a total cost over the entire trees (by summing the cost at each node) of \(O(n_n_^\log(n_))\) .
What are all the various decision tree algorithms and how do they differ from each other? Which one is implemented in scikit-learn?
Various decision tree algorithms#
ID3 (Iterative Dichotomiser 3) was developed in 1986 by Ross Quinlan. The algorithm creates a multiway tree, finding for each node (i.e. in a greedy manner) the categorical feature that will yield the largest information gain for categorical targets. Trees are grown to their maximum size and then a pruning step is usually applied to improve the ability of the tree to generalize to unseen data.
C4.5 is the successor to ID3 and removed the restriction that features must be categorical by dynamically defining a discrete attribute (based on numerical variables) that partitions the continuous attribute value into a discrete set of intervals. C4.5 converts the trained trees (i.e. the output of the ID3 algorithm) into sets of if-then rules. The accuracy of each rule is then evaluated to determine the order in which they should be applied. Pruning is done by removing a rule’s precondition if the accuracy of the rule improves without it.
C5.0 is Quinlan’s latest version release under a proprietary license. It uses less memory and builds smaller rulesets than C4.5 while being more accurate.
CART (Classification and Regression Trees) is very similar to C4.5, but it differs in that it supports numerical target variables (regression) and does not compute rule sets. CART constructs binary trees using the feature and threshold that yield the largest information gain at each node.
scikit-learn uses an optimized version of the CART algorithm; however, the scikit-learn implementation does not support categorical variables for now.
Given training vectors \(x_i \in R^n\) , i=1,…, l and a label vector \(y \in R^l\) , a decision tree recursively partitions the feature space such that the samples with the same labels or similar target values are grouped together.
Let the data at node \(m\) be represented by \(Q_m\) with \(n_m\) samples. For each candidate split \(\theta = (j, t_m)\) consisting of a feature \(j\) and threshold \(t_m\) , partition the data into \(Q_m^(\theta)\) and \(Q_m^(\theta)\) subsets
\[ \beginThe quality of a candidate split of node \(m\) is then computed using an impurity function or loss function \(H()\) , the choice of which depends on the task being solved (classification or regression)
\[G(Q_m, \theta) = \frac> H(Q_m^(\theta)) + \frac> H(Q_m^(\theta))\]Select the parameters that minimises the impurity \[\theta^* = \operatornameRecurse for subsets \(Q_m^(\theta^*)\) and \(Q_m^(\theta^*)\) until the maximum allowable depth is reached, \(n_m < \min_\) or \(n_m = 1\) .
If a target is a classification outcome taking on values 0,1,…,K-1, for node \(m\) , let
\[p_be the proportion of class k observations in node \(m\) . If \(m\) is a terminal node, predict_proba for this region is set to \(p_\) . Common measures of impurity are the following.
\[H(Q_m) = \sum_k p_Log Loss or Entropy:
\[H(Q_m) = - \sum_k p_The entropy criterion computes the Shannon entropy of the possible classes. It takes the class frequencies of the training data points that reached a given leaf \(m\) as their probability. Using the Shannon entropy as tree node splitting criterion is equivalent to minimizing the log loss (also known as cross-entropy and multinomial deviance) between the true labels \(y_i\) and the probabilistic predictions \(T_k(x_i)\) of the tree model \(T\) for class \(k\) .
To see this, first recall that the log loss of a tree model \(T\) computed on a dataset \(D\) is defined as follows:
\[\mathrmwhere \(D\) is a training dataset of \(n\) pairs \((x_i, y_i)\) .
In a classification tree, the predicted class probabilities within leaf nodes are constant, that is: for all \((x_i, y_i) \in Q_m\) , one has: \(T_k(x_i) = p_\) for each class \(k\) .
This property makes it possible to rewrite \(\mathrm(D, T)\) as the sum of the Shannon entropies computed for each leaf of \(T\) weighted by the number of training data points that reached each leaf:
\[\mathrmIf the target is a continuous value, then for node \(m\) , common criteria to minimize as for determining locations for future splits are Mean Squared Error (MSE or L2 error), Poisson deviance as well as Mean Absolute Error (MAE or L1 error). MSE and Poisson deviance both set the predicted value of terminal nodes to the learned mean value \(\bar_m\) of the node whereas the MAE sets the predicted value of terminal nodes to the median \(median(y)_m\) .
Mean Squared Error:
\[ \beginHalf Poisson deviance:
\[H(Q_m) = \frac<1> \sum_ (y \log\frac<\bar_m> - y + \bar_m)\]Setting criterion="poisson" might be a good choice if your target is a count or a frequency (count per some unit). In any case, \(y >= 0\) is a necessary condition to use this criterion. Note that it fits much slower than the MSE criterion.
Mean Absolute Error:
\[ \beginNote that it fits much slower than the MSE criterion.
DecisionTreeClassifier and DecisionTreeRegressor have built-in support for missing values when splitter='best' and criterion is 'gini' , 'entropy ’, or 'log_loss' , for classification or 'squared_error' , 'friedman_mse' , or 'poisson' for regression.
For each potential threshold on the non-missing data, the splitter will evaluate the split with all the missing values going to the left node or the right node.
Decisions are made as follows:
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([0, 1, 6, np.nan]).reshape(-1, 1) >>> y = [0, 0, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> tree.predict(X) array([0, 0, 1, 1])
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([np.nan, -1, np.nan, 1]).reshape(-1, 1) >>> y = [0, 0, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> X_test = np.array([np.nan]).reshape(-1, 1) >>> tree.predict(X_test) array([1])
>>> from sklearn.tree import DecisionTreeClassifier >>> import numpy as np >>> X = np.array([0, 1, 2, 3]).reshape(-1, 1) >>> y = [0, 1, 1, 1] >>> tree = DecisionTreeClassifier(random_state=0).fit(X, y) >>> X_test = np.array([np.nan]).reshape(-1, 1) >>> tree.predict(X_test) array([1])
Minimal cost-complexity pruning is an algorithm used to prune a tree to avoid over-fitting, described in Chapter 3 of [BRE] . This algorithm is parameterized by \(\alpha\ge0\) known as the complexity parameter. The complexity parameter is used to define the cost-complexity measure, \(R_\alpha(T)\) of a given tree \(T\) :
\[R_\alpha(T) = R(T) + \alpha|\widetildewhere \(|\widetilde|\) is the number of terminal nodes in \(T\) and \(R(T)\) is traditionally defined as the total misclassification rate of the terminal nodes. Alternatively, scikit-learn uses the total sample weighted impurity of the terminal nodes for \(R(T)\) . As shown above, the impurity of a node depends on the criterion. Minimal cost-complexity pruning finds the subtree of \(T\) that minimizes \(R_\alpha(T)\) .
The cost complexity measure of a single node is \(R_\alpha(t)=R(t)+\alpha\) . The branch, \(T_t\) , is defined to be a tree where node \(t\) is its root. In general, the impurity of a node is greater than the sum of impurities of its terminal nodes, \(R(T_t)(t)=\frac<|T|-1>\) . A non-terminal node with the smallest value of \(\alpha_\) is the weakest link and will be pruned. This process stops when the pruned tree’s minimal \(\alpha_\) is greater than the ccp_alpha parameter.
L. Breiman, J. Friedman, R. Olshen, and C. Stone. Classification and Regression Trees. Wadsworth, Belmont, CA, 1984.
1.11. Ensembles: Gradient boosting, random forests, bagging, voting, stacking